研究分野

研究分野の画像

中田研究室では, 次の3つの分野の研究を行っています.

これらの分野は完全に独立しているわけでなく, 共通している部分が沢山あります. 実際には, これらの分野を横断して研究をしていると言ってよいでしょう. 以下では, この3つのキーワードを軸に研究の紹介をしていきます.


オペレーションズ・リサーチ

オペレーションズ・リサーチとは, 世の中の大小の組織レベルで生じる様々な問題点に対し, それを数理モデルで表現し解析することにより, 合理的な解決策を導き出す手法です. Operations Researchを略してORとも呼ばれています. 最適化技術の発展に伴って, 社会の様々な場面でオペレーションズ・リサーチが利用されるようになり, 多方面にマーケットが広がっています. 機械学習と連携させることも多いです.

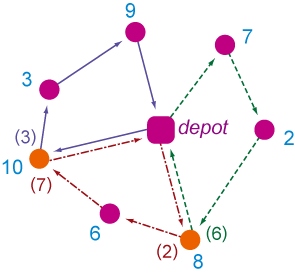
配送計画問題の概念図

研究室では企業との共同研究により次のような事例研究を行ってきました.

  • 工場で生産した車両の全国のディーラーへの輸送計画
  • 小売店のスタッフの勤務交番表や作業分担表の自動作成
  • 巨大倉庫での効率的な商品ピッキング
  • 年金の運用など長期に渡るアセットアロケーション
  • 受付案内システムの待ち時間の分析と人員最適化
  • 客室数を考慮したお薦めホテルの個別メール配信
  • 印刷会社における多種多様な印刷注文の作業スケジューリング
教科書で説明されているような例題と違い, 現実の問題は複雑で曖昧で変化を伴う事が多く, 一筋縄では解決策を導けません. そのため, 現場をよく観察し, 先方とディスカッションを重ねながら, モデルとアルゴリズム両方を少しずつ改善していきます. このとき, モデルの正確性とアルゴリズムの効率性はトレードオフとなることが多く, その解決法を頭を絞って考えます. 幾多の困難を乗り越え, 実務に役立つ解決策を捻出するプロセスは, 実学であるオペレーションズ・リサーチの醍醐味です.


機械学習

Wikipediaによると, 機械学習とは『ある程度の数のサンプルデータ集合を対象に解析を行い, そのデータから有用な規則, ルール, 知識表現, 判断基準などを抽出する』手法と解説されています. もともと人工知能のー分野として研究が続けられていましたが, ディープラーニングの登場と共に大きく発展しています.

近年, コンピュータの導入やインターネットの普及に伴い, 顧客の行動・購買履歴, ドキュメントデータ, 画像データなどのデジタル情報を大量に保有することは珍しくなくなりました. これらのビッグデータから機械学習によって有益な知見を得ることが, ますます重要になっています.

サポートベクターマシンの概念図

研究室では企業との共同研究による次のような事例研究を行ってきました.

  • 電子カルテの分析による適切な治療の推薦
  • 機械の稼働情報を用いた故障予測
  • リスティング広告における広告文自動生成
  • オルタナティブデータを用いた株価予想
  • 有価証券報告書のテキストマイニングによる特徴抽出
  • 特許文書に対するFIの自動付加

得られた知見を組織の活動に利用するという点では, オペレーションズ・リサーチと関連が深いです. また, データを使った学習は, 結局のところパラメタの最適化に帰着できます.

これまでに, 上記の共同研究やデータ解析コンペティションへの参加によって, 17セットの大規模な実データの分析を行い (2021年現在), それらの成果を学術誌や学会で発表してきました. 扱ったデータは, 商品の購買履歴・Webサイトのアクセスログ・機械の稼働情報・大量の日本語文書など様々です. 現在は高性能な機械学習用ツールがフリーで公開されており, Pythonさえ使えれば対象データに標準的な機械学習手法を適用することは簡単です. しかし, それだけで興味深い結果が得られることはほとんどありません. 有用な知見を得るためには, データに合わせた様々な工夫・改良・新しい学習モデルの提案などが必要となります.

データ解析コンペティションへの参加については, オペレーションズ・リサーチ誌に掲載された解説記事もご覧ください.


最適化

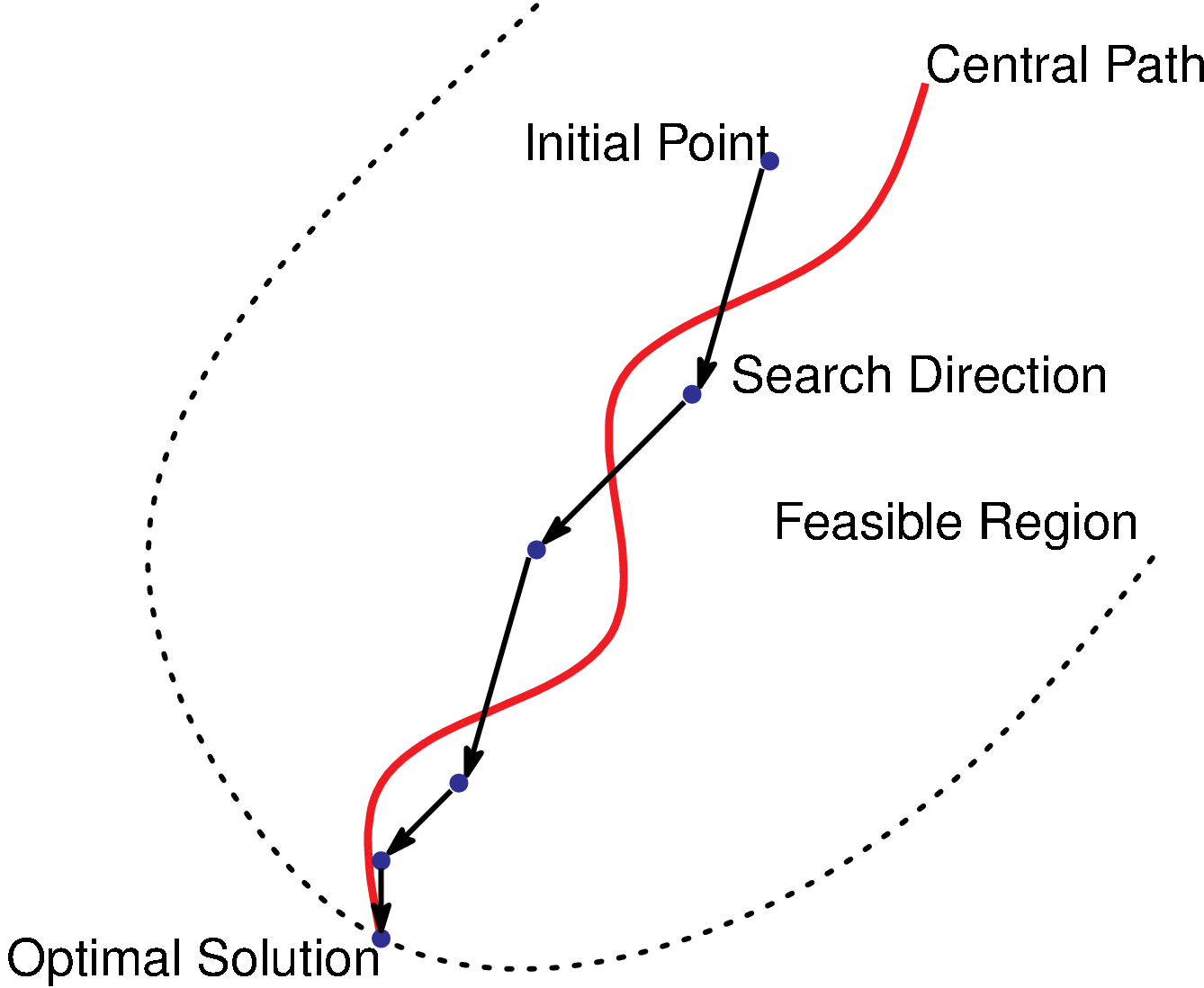
内点法の概念図

最適化とは, 制約条件を満たすものの中で, 目的関数を最小 (最大) にする解を求める技術です. 機械の最適制御, 磁気シールドの設計, 建築物の構造設計, ポートフォリオ選択, 力学における変分原理 (最小作用の原理), 分子の基底エネルギー計算, 統計における最尤推定など, 様々な理学・工学分野で最適化計算が行われてきました. オペレーションズ・リサーチや機械学習で扱うモデルの多くも最適化問題になります. 最適化は分野横断型技術であり, 機械・電気・建築・土木・材料・金融・医学・物理・化学などの各分野を縦糸とすると, 横糸的な性格を持っています.

ムーアの法則で示されるような指数関数的な計算機性能の向上や, 最適化アルゴリズムの目覚ましい発展により, 10年前や20年前と比べ, 現在では相当大規模な最適化問題を解くことが可能となってきました. しかしながら, 更に大規模な問題を高速に最適化したい, という社会からの欲求は尽きることはありません.

研究室では, よりよい最適化法について模索し, 革新的なアルゴリズムの発見やそれを実装した最適化ソフトウェアの開発を行っています. そのためには, 最適化問題の数理的構造を理解する必要があります. また, 計算機で効率的に情報を処理するためには, 「アルゴリズムとデータ構造」や「ハイパフォーマンスコンピューティング」的な技術も要求されます.

これまでに行ってきた研究の詳細は, こちらをご覧下さい.